Progresia geometrică găsiți b1. Progresie geometrică. Ghid cuprinzător cu exemple (2020). Lecție și prezentare pe tema: „Secvențe de numere. Progresie geometrică”

Lecție și prezentare pe tema: „Secvențe de numere. Progresie geometrică”

Materiale suplimentare
Dragi utilizatori, nu uitați să lăsați comentariile, recenziile, urările! Toate materialele au fost verificate de un program antivirus.

Ajutoare educaționale și simulatoare în magazinul online Integral pentru clasa a 9-a
Puteri și rădăcini Funcții și grafice

Băieți, astăzi ne vom familiariza cu un alt tip de progresie.
Tema lecției de astăzi este progresia geometrică.

Progresie geometrică

Definiţie. O succesiune numerică în care fiecare termen, începând cu al doilea, este egal cu produsul celui precedent și un număr fix se numește progresie geometrică.
Să definim secvența noastră recursiv: $b_(1)=b$, $b_(n)=b_(n-1)*q$,
unde b și q sunt anumite numere date. Numărul q se numește numitorul progresiei.

Exemplu. 1,2,4,8,16... O progresie geometrică în care primul termen este egal cu unu și $q=2$.

Exemplu. 8,8,8,8... O progresie geometrică în care primul termen este egal cu opt,
și $q=1$.

Exemplu. 3,-3,3,-3,3... Progresie geometrică în care primul termen este egal cu trei,
și $q=-1$.

Progresia geometrică are proprietățile monotoniei.
Dacă $b_(1)>0$, $q>1$,
atunci secvența crește.
Dacă $b_(1)>0$, $0 Secvența se notează de obicei sub forma: $b_(1), b_(2), b_(3), ..., b_(n), ...$.

La fel ca într-o progresie aritmetică, dacă într-o progresie geometrică numărul de elemente este finit, atunci progresia se numește progresie geometrică finită.

$b_(1), b_(2), b_(3), ..., b_(n-2), b_(n-1), b_(n)$.
Rețineți că, dacă o secvență este o progresie geometrică, atunci șirul de pătrate de termeni este, de asemenea, o progresie geometrică. În a doua secvență, primul termen este egal cu $b_(1)^2$, iar numitorul este egal cu $q^2$.

Formula pentru al n-lea termen al unei progresii geometrice

Progresia geometrică poate fi specificată și sub formă analitică. Să vedem cum să facem asta:
$b_(1)=b_(1)$.
$b_(2)=b_(1)*q$.
$b_(3)=b_(2)*q=b_(1)*q*q=b_(1)*q^2$.
$b_(4)=b_(3)*q=b_(1)*q^3$.
$b_(5)=b_(4)*q=b_(1)*q^4$.
Observăm cu ușurință modelul: $b_(n)=b_(1)*q^(n-1)$.
Formula noastră se numește „formula celui de-al n-lea termen al unei progresii geometrice”.

Să revenim la exemplele noastre.

Exemplu. 1,2,4,8,16... O progresie geometrică al cărei prim termen este egal cu unu,
și $q=2$.
$b_(n)=1*2^(n)=2^(n-1)$.

Exemplu. 16,8,4,2,1,1/2... O progresie geometrică în care primul termen este egal cu șaisprezece și $q=\frac(1)(2)$.
$b_(n)=16*(\frac(1)(2))^(n-1)$.

Exemplu. 8,8,8,8... O progresie geometrică în care primul termen este egal cu opt și $q=1$.
$b_(n)=8*1^(n-1)=8$.

Exemplu. 3,-3,3,-3,3... O progresie geometrică în care primul termen este egal cu trei și $q=-1$.
$b_(n)=3*(-1)^(n-1)$.

Exemplu. Având în vedere o progresie geometrică $b_(1), b_(2), …, b_(n), … $.
a) Se știe că $b_(1)=6, q=3$. Găsiți $b_(5)$.
b) Se știe că $b_(1)=6, q=2, b_(n)=768$. Găsiți n.
c) Se știe că $q=-2, b_(6)=96$. Găsiți $b_(1)$.
d) Se știe că $b_(1)=-2, b_(12)=4096$. Găsiți q.

Soluţie.
a) $b_(5)=b_(1)*q^4=6*3^4=486$.
b) $b_n=b_1*q^(n-1)=6*2^(n-1)=768$.
$2^(n-1)=\frac(768)(6)=128$, deoarece $2^7=128 => n-1=7; n=8$.
c) $b_(6)=b_(1)*q^5=b_(1)*(-2)^5=-32*b_(1)=96 => b_(1)=-3$.
d) $b_(12)=b_(1)*q^(11)=-2*q^(11)=4096 => q^(11)=-2048 => q=-2$.

Exemplu. Diferența dintre termenii al șaptelea și al cincilea al progresiei geometrice este 192, suma celor cinci și al șaselea termeni ale progresiei este 192. Aflați al zecelea termen al acestei progresii.

Soluţie.
Știm că: $b_(7)-b_(5)=192$ și $b_(5)+b_(6)=192$.
Mai știm: $b_(5)=b_(1)*q^4$; $b_(6)=b_(1)*q^5$; $b_(7)=b_(1)*q^6$.
Apoi:
$b_(1)*q^6-b_(1)*q^4=192$.
$b_(1)*q^4+b_(1)*q^5=192$.
Am primit un sistem de ecuații:
$\begin(cases)b_(1)*q^4(q^2-1)=192\\b_(1)*q^4(1+q)=192\end(cases)$.
Echivalând ecuațiile noastre obținem:
$b_(1)*q^4(q^2-1)=b_(1)*q^4(1+q)$.
$q^2-1=q+1$.
$q^2-q-2=0$.
Avem două soluții q: $q_(1)=2, q_(2)=-1$.
Înlocuiți secvențial în a doua ecuație:
$b_(1)*2^4*3=192 => b_(1)=4$.
$b_(1)*(-1)^4*0=192 =>$ nicio soluție.
Am obținut că: $b_(1)=4, q=2$.
Să găsim al zecelea termen: $b_(10)=b_(1)*q^9=4*2^9=2048$.

Suma unei progresii geometrice finite

Să avem o progresie geometrică finită. Să calculăm, la fel ca pentru o progresie aritmetică, suma termenilor săi.

Să fie dată o progresie geometrică finită: $b_(1),b_(2),…,b_(n-1),b_(n)$.
Să introducem denumirea pentru suma termenilor săi: $S_(n)=b_(1)+b_(2)+⋯+b_(n-1)+b_(n)$.
În cazul în care $q=1$. Toți termenii progresiei geometrice sunt egali cu primul termen, atunci este evident că $S_(n)=n*b_(1)$.
Să luăm acum în considerare cazul $q≠1$.
Să înmulțim suma de mai sus cu q.
$S_(n)*q=(b_(1)+b_(2)+⋯+b_(n-1)+b_(n))*q=b_(1)*q+b_(2)*q+⋯ +b_(n-1)*q+b_(n)*q=b_(2)+b_(3)+⋯+b_(n)+b_(n)*q$.
Nota:
$S_(n)=b_(1)+(b_(2)+⋯+b_(n-1)+b_(n))$.
$S_(n)*q=(b_(2)+⋯+b_(n-1)+b_(n))+b_(n)*q$.

$S_(n)*q-S_(n)=(b_(2)+⋯+b_(n-1)+b_(n))+b_(n)*q-b_(1)-(b_(2) )+⋯+b_(n-1)+b_(n))=b_(n)*q-b_(1)$.

$S_(n)(q-1)=b_(n)*q-b_(1)$.

$S_(n)=\frac(b_(n)*q-b_(1))(q-1)=\frac(b_(1)*q^(n-1)*q-b_(1)) (q-1)=\frac(b_(1)(q^(n)-1))(q-1)$.

$S_(n)=\frac(b_(1)(q^(n)-1))(q-1)$.

Am obținut formula pentru suma unei progresii geometrice finite.

Exemplu.
Aflați suma primilor șapte termeni ai unei progresii geometrice al cărei prim termen este 4 și numitorul este 3.

Soluţie.
$S_(7)=\frac(4*(3^(7)-1))(3-1)=2*(3^(7)-1)=4372$.

Exemplu.
Aflați al cincilea termen al progresiei geometrice care este cunoscut: $b_(1)=-3$; $b_(n)=-3072$; $S_(n)=-4095$.

Soluţie.
$b_(n)=(-3)*q^(n-1)=-3072$.
$q^(n-1)=1024$.
$q^(n)=1024q$.

$S_(n)=\frac(-3*(q^(n)-1))(q-1)=-4095$.
$-4095(q-1)=-3*(q^(n)-1)$.
$-4095(q-1)=-3*(1024q-1)$.
$1365q-1365=1024q-1$.
341$ q=1364$.
$q=4$.
$b_5=b_1*q^4=-3*4^4=-3*256=-768$.

Proprietatea caracteristică a progresiei geometrice

Băieți, se dă o progresie geometrică. Să ne uităm la cei trei membri consecutivi ai săi: $b_(n-1),b_(n),b_(n+1)$.
Stim ca:
$\frac(b_(n))(q)=b_(n-1)$.
$b_(n)*q=b_(n+1)$.
Apoi:
$\frac(b_(n))(q)*b_(n)*q=b_(n)^(2)=b_(n-1)*b_(n+1)$.
$b_(n)^(2)=b_(n-1)*b_(n+1)$.
Dacă progresia este finită, atunci această egalitate este valabilă pentru toți termenii, cu excepția primului și ultimului.
Dacă nu se știe dinainte ce formă are șirul, dar se știe că: $b_(n)^(2)=b_(n-1)*b_(n+1)$.
Apoi putem spune cu siguranță că aceasta este o progresie geometrică.

O secvență de numere este o progresie geometrică numai atunci când pătratul fiecărui membru este egal cu produsul celor două elemente adiacente ale progresiei. Nu uitați că pentru o progresie finită această condiție nu este îndeplinită pentru primul și ultimul termen.

Să ne uităm la această identitate: $\sqrt(b_(n)^(2))=\sqrt(b_(n-1)*b_(n+1))$.
$|b_(n)|=\sqrt(b_(n-1)*b_(n+1))$.
$\sqrt(a*b)$ se numește media geometrică a numerelor a și b.

Modulul oricărui termen al unei progresii geometrice este egal cu media geometrică a celor doi termeni adiacenți ai săi.

Exemplu.
Găsiți x astfel încât $x+2; 2x+2; 3x+3$ au fost trei termeni consecutivi ai unei progresii geometrice.

Soluţie.
Să folosim proprietatea caracteristică:
$(2x+2)^2=(x+2)(3x+3)$.
$4x^2+8x+4=3x^2+3x+6x+6$.
$x^2-x-2=0$.
$x_(1)=2$ și $x_(2)=-1$.
Să substituim succesiv soluțiile noastre în expresia originală:
Cu $x=2$ am obtinut sirul: 4;6;9 – o progresie geometrica cu $q=1.5$.
Pentru $x=-1$, obținem succesiunea: 1;0;0.
Răspuns: $x=2.$

Probleme de rezolvat independent

1. Aflați al optulea prim termen al progresiei geometrice 16;-8;4;-2….
2. Aflați al zecelea termen al progresiei geometrice 11,22,44….
3. Se știe că $b_(1)=5, q=3$. Găsiți $b_(7)$.
4. Se știe că $b_(1)=8, q=-2, b_(n)=512$. Găsiți n.
5. Aflați suma primilor 11 termeni ai progresiei geometrice 3;12;48….
6. Găsiți x astfel încât $3x+4; 2x+4; x+5$ sunt trei termeni consecutivi ai unei progresii geometrice.

O progresie geometrică este o succesiune numerică, al cărei prim termen este diferit de zero și fiecare termen ulterior este egal cu termenul anterior înmulțit cu același număr diferit de zero. Progresia geometrică se notează b1,b2,b3, …, bn, …

Proprietăți ale progresiei geometrice

Raportul dintre orice termen al erorii geometrice și termenul anterior este egal cu același număr, adică b2/b1 = b3/b2 = b4/b3 = ... = bn/b(n-1) = b( n+1)/bn = … . Aceasta rezultă direct din definiția unei progresii aritmetice. Acest număr se numește numitorul unei progresii geometrice. De obicei, numitorul unei progresii geometrice este notat cu litera q.

Una dintre modalitățile de a specifica o progresie geometrică este de a specifica primul său termen b1 și numitorul erorii geometrice q. De exemplu, b1=4, q=-2. Aceste două condiții definesc progresia geometrică 4, -8, 16, -32, ….

Dacă q>0 (q nu este egal cu 1), atunci progresia este o secvență monotonă. De exemplu, secvența, 2, 4,8,16,32, ... este o secvență crescătoare monoton (b1=2, q=2).

Dacă numitorul în eroarea geometrică este q=1, atunci toți termenii progresiei geometrice vor fi egali între ei. În astfel de cazuri, se spune că progresia este o secvență constantă.

Formula pentru al n-lea termen al progresiei

Pentru ca o succesiune de numere (bn) sa fie o progresie geometrica, este necesar ca fiecare dintre membrii sai, incepand de la al doilea, sa fie media geometrica a membrilor invecinati. Adică, este necesar să se îndeplinească următoarea ecuație - (b(n+1))^2 = bn * b(n+2), pentru orice n>0, unde n aparține mulțimii numere naturale N.

Formula pentru al n-lea termen al progresiei geometrice este:

bn=b1*q^(n-1), unde n aparține mulțimii numerelor naturale N.

Să ne uităm la un exemplu simplu:

În progresia geometrică b1=6, q=3, n=8 găsiți bn.

Să folosim formula pentru al n-lea termen al unei progresii geometrice.

Conceptul de progresie geometrică

Progresia geometrică se notează b1,b2,b3, …, bn, ….

Suma unei progresii geometrice infinite pentru |q|<1

Dacă q>0 (q nu este egal cu 1), atunci progresia este o secvență monotonă. De exemplu, secvența, 2, 4,8,16,32, ... este o secvență crescătoare monoton (b1=2, q=2).

Dacă numitorul în eroarea geometrică este q=1, atunci toți termenii progresiei geometrice vor fi egali între ei. În astfel de cazuri, se spune că progresia este o secvență constantă.

Pentru ca o succesiune de numere (bn) sa fie o progresie geometrica, este necesar ca fiecare dintre membrii sai, incepand de la al doilea, sa fie media geometrica a membrilor invecinati. Adică, este necesar să se îndeplinească următoarea ecuație
(b(n+1))^2 = bn * b(n+2), pentru orice n>0, unde n aparține mulțimii numerelor naturale N.

Acum să punem (Xn) - o progresie geometrică. Numitorul progresiei geometrice q, și |q|∞).
Dacă notăm acum cu S suma unei progresii geometrice infinite, atunci se va aplica următoarea formulă:
S=x1/(1-q).

Să ne uităm la un exemplu simplu:

Aflați suma progresiei geometrice infinite 2, -2/3, 2/9, - 2/27, ….

Pentru a găsi S, folosim formula pentru suma unei progresii aritmetice infinite. |-1/3|< 1. x1 = 2. S=2/(1-(-1/3)) = 3/2.

Lecție pe tema „Progresie geometrică în scădere infinită”

Obiectivul lecției: introducerea elevilor într-un nou tip de succesiune – o progresie geometrică infinit descrescătoare.

Sarcini:

formularea unei idei inițiale a limitei unei secvențe numerice; cunoașterea unui alt mod de a converti fracții periodice infinite în fracții obișnuite folosind formula pentru suma unei progresii geometrice infinit descrescătoare;

dezvoltarea calităților intelectuale ale personalității școlarilor, cum ar fi gândirea logică, capacitatea de a face acțiuni evaluative și generalizarea;

stimularea activității, asistenței reciproce, colectivismului și interesului pentru subiect.

Echipament: clasa de calculatoare, proiector, ecran.

Tip de lecție: lectie – invatare subiect nou.

Progresul lecției

eu . Org. moment. Prezentați subiectul și scopul lecției.

II . Actualizarea cunoștințelor elevilor.1. Verificarea temelor.

1) Verificarea formulelor de bază referitoare la progresiile aritmetice și geometrice. Doi elevi pregătesc note despre formule la tablă.

2) Restul elevilor o fac dictare matematică pe tema „Formulele sumei”.

Misiuni:

№1. Aflați suma primilor cinci termeni ai unei progresii aritmetice dacă primul său termen este 6 (prima opțiune), -20 (a doua opțiune), iar al cincilea termen este -6 (prima opțiune), 20 (a doua opțiune).

№2. Aflați suma primilor cinci termeni ai unei progresii aritmetice dacă primul său termen este -20 (prima opțiune), 6 (a doua opțiune), iar diferența este 10 (prima opțiune), -3 (a doua opțiune).

№3. Aflați suma primilor cinci termeni ai unei progresii geometrice dacă primul său termen este egal cu 1 (prima opțiune), -1 (a doua opțiune), iar numitorul este -2 (prima opțiune), 2 (a doua opțiune).

La sfârșitul dictatului, munca a doi elevi este verificată selectiv pentru evaluare, ceilalți efectuează un autotest folosind soluții gata făcute scrise pe clapele tablei.

Solutii:

Misiuni

1. Progresia aritmetică este dată de formula o n = 7 – 4 n. Găsi o 10 . (-33)

2. În progresie aritmetică o 3 = 7 Şi o 5 = 1 . Găsi o 4 . (4)

3. În progresie aritmetică o 3 = 7 Şi o 5 = 1 . Găsi o 17 . (-35)

4. În progresie aritmetică o 3 = 7 Şi o 5 = 1 . Găsi S 17 . (-187)

5. Pentru progresie geometrică
găsiți al cincilea termen.

6. Pentru progresie geometrică
găsi n al-lea membru.

7. Exponenţial b 3 = 8 Şi b 5 = 2 . Găsi b 4 . (4)

8. Exponenţial b 3 = 8 Şi b 5 = 2 . Găsi b 1 Şi q .

9. Exponenţial b 3 = 8 Şi b 5 = 2 . Găsi S 5 . (62)

III . Învățarea unui subiect nou(demonstrație de prezentare).

Să considerăm un pătrat cu latura egală cu 1. Să desenăm un alt pătrat a cărui latură este jumătate din dimensiunea primului pătrat, apoi altul a cărui latură este jumătate din a doua, apoi următorul etc. De fiecare dată când latura noului pătrat este egală cu jumătate din cea precedentă.

Ca rezultat, am primit o succesiune de laturi de pătrate formând o progresie geometrică cu numitorul .

Și, ceea ce este foarte important, cu cât construim mai multe astfel de pătrate, cu atât latura pătratului va fi mai mică. De exemplu,

Aceste. Pe măsură ce numărul n crește, termenii progresiei se apropie de zero.

Folosind această figură, puteți lua în considerare o altă secvență.

De exemplu, succesiunea ariilor pătratelor:

. Și, din nou, dacă n crește la nesfârșit, apoi zona se apropie de zero cât de aproape doriți.

Să ne uităm la un alt exemplu. Un triunghi echilateral cu laturile egale cu 1 cm. Să construim următorul triunghi cu vârfurile în mijlocul laturilor primului triunghi, conform teoremei despre linia mediană a triunghiului - latura celui de-al 2-lea este egală cu jumătatea laturii primului, latura celui de-al 3-lea este egal cu jumătate din latura celui de-al 2-lea etc. Din nou obținem o succesiune de lungimi ale laturilor triunghiurilor.

la
.

Dacă luăm în considerare o progresie geometrică cu numitor negativ.

Apoi, din nou, cu un număr tot mai mare n termenii progresiei se apropie de zero.

Să fim atenți la numitorii acestor secvențe. Peste tot numitorii erau mai mici de 1 în valoare absolută.

Putem concluziona: o progresie geometrică va fi infinit descrescătoare dacă modulul numitorului său este mai mic de 1.

Lucru frontal.

Definiţie:

Se spune că o progresie geometrică este infinit descrescătoare dacă modulul numitorului său este mai mic de unu.
.

Folosind definiția, puteți decide dacă o progresie geometrică este în scădere infinit sau nu.

Sarcină

Este succesiunea o progresie geometrică infinit descrescătoare dacă este dată de formula:

;
.

Soluţie:

. Vom găsi q .

;
;
;
.

această progresie geometrică este infinit în scădere.

b) această succesiune nu este o progresie geometrică infinit descrescătoare.

Să considerăm un pătrat cu latura egală cu 1. Împărțiți-l în jumătate, una dintre jumătăți în jumătate etc. Aricele tuturor dreptunghiurilor rezultate formează o progresie geometrică infinit descrescătoare:

Suma ariilor tuturor dreptunghiurilor obținute în acest fel va fi egală cu aria primului pătrat și egală cu 1.

Dar în partea stângă a acestei egalități se află suma unui număr infinit de termeni.

Să considerăm suma primilor n termeni.

Conform formulei pentru suma primilor n termeni ai unei progresii geometrice, este egal cu .

Dacă n crește fără limită, atunci

sau
. De aceea
, adică
.

Suma unei progresii geometrice infinit descrescătoare există o limită de secvență S 1 , S 2 , S 3 , …, S n , … .

De exemplu, pentru progresie
,

Deoarece

Suma unei progresii geometrice infinit descrescătoare poate fi găsit folosind formula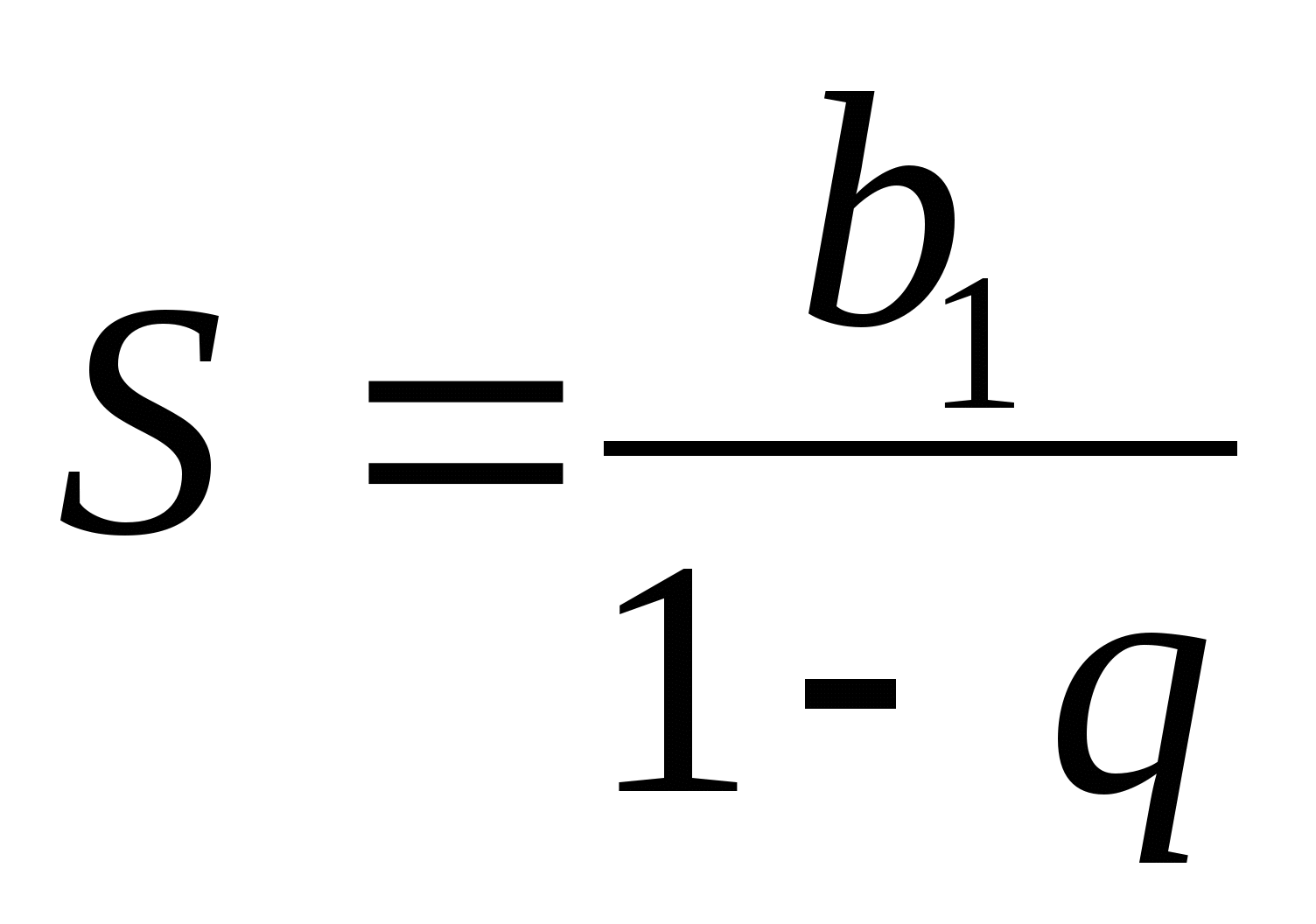
.

III . Înțelegerea și consolidarea(finalizarea sarcinilor).

Sarcina nr. 2. Aflați suma unei progresii geometrice infinit descrescătoare, primul termen fiind 3 și al doilea termen fiind 0,3.

Soluţie:

Sarcina nr. 3. manual, p. 160, nr. 433(1)

Aflați suma unei progresii geometrice infinit descrescătoare:

Soluţie:

Sarcina nr. 4. Scrie o periodică infinită zecimal 0,(5) ca o fracție comună.

1a metoda. Fie x=0,(5)= 0,555... / 10 Metoda a 2-a. 0,(5)=0,555…=

Sarcina nr. 5. manual, p. 162, nr. 445(3) (soluție independentă)

Scrieți fracția zecimală periodică infinită 0,(12) ca o fracție comună.

Răspuns: 0,(12)= 4/33.

IV . Rezumând.

Cu ce secvență v-ați familiarizat astăzi?

Definiți o progresie geometrică infinit descrescătoare.

Cum se demonstrează că o progresie geometrică este în scădere infinită?

Dați formula pentru suma unei progresii geometrice infinit descrescătoare.

V . Teme pentru acasă.

Anna Malkova

Progresie geometrică este o succesiune, al cărei termen, începând cu al doilea, este egal cu produsul termenului anterior și un număr fix q:

Număr fix q numit numitorul unei progresii geometrice.

Formula pentru al n-lea termen al unei progresii geometrice:

Formula pentru suma primei membrii progresiei geometrice se calculează prin formula:

Pătratul fiecărui termen al progresiei geometrice, începând cu al doilea, este egal cu produsul celor vecini:

1. Algele cresc pe suprafața lacului. În decurs de o zi, fiecare algă este împărțită în jumătate și, în loc de o algă, apar două. După încă o zi, fiecare dintre algele rezultate este împărțită în jumătate și așa mai departe. După 30 de zile, lacul a fost complet acoperit de alge. Cât a durat până când lacul a fost plin pe jumătate?

Răspunsul este paradoxal: după 29 de zile.

Această problemă este cel mai bine rezolvată „de la sfârșit”. Aici în fața ta este un lac plin de alge. Ce sa întâmplat cu o zi în urmă? Evident, erau jumătate din câte alge, adică lacul era pe jumătate acoperit cu ele.

În fiecare zi erau de două ori mai multe alge în lac, adică numărul lor creștea în progresie geometrică.

2. Examen de stat unificat) Omul de afaceri Bublikov a primit un profit de 5.000 de ruble în 2000. În fiecare an următor, profiturile sale au crescut cu 300% față de anul precedent. Câte ruble a câștigat Bublikov în 2003?

Profitul lui Bublikov în 2000 a fost mic. Dar în fiecare an profitul a crescut cu 300%, adică de 4 ori față de anul precedent. Progresie geometrică! Căutăm al patrulea membru al ei:

3. (Problema de examinare de stat unificată) Compania Alpha a început să investească într-o industrie promițătoare în 2001, cu un capital de 3.000 USD. În fiecare an, din 2002, a realizat un profit care a reprezentat 100% din capitalul anului precedent. Iar Compania Beta a început să investească într-o altă industrie în 2003, cu un capital de 6.000 USD și, din 2004, a realizat un profit anual de 200% din capitalul anului precedent. Cu câți dolari era capitalul unei companii mai mare decât capitalul celeilalte la sfârșitul anului 2006, dacă profiturile nu erau retrase din circulație?

Să definim conceptele de bază ale problemei.

Capitalul companiei– totalitatea tuturor fondurilor disponibile companiei.

Profit– diferența dintre venituri și cheltuieli (costuri).

Dacă în 2002 profitul companiei Alpha este de 100% din capitalul anului precedent, înseamnă că capitalul companiei Alpha s-a dublat pe parcursul anului. La fel, capitalul Alpha se dublează în 2003, 2004, 2005 și 2006, adică a fost de mii de dolari în 2006.

Capitalul companiei Beta crește de 3 ori anual. În 2006, a crescut de câteva ori față de 2003 și s-a ridicat la dolari.

Acesta este cu 66 de mii de dolari mai mult decât capitalul companiei Alpha.

Progresie geometrică în scădere infinită

O progresie geometrică al cărei numitor este |q|<1, называется бесконечно убывающей.

Un exemplu de progresie geometrică infinit descrescătoare.

Care este suma sa?

Să desenăm un dreptunghi cu zonă 1. Adăugăm la el zone cu zonă

La ce tinde aria figurii rezultate cu o creștere infinită a n, adică cu adăugarea unor suprafețe din ce în ce mai mici? Evident, cu doi.

Suma unei progresii geometrice infinit descrescătoare este un număr care se găsește prin formula:

Există o glumă matematică și acum o vei înțelege.

Un număr infinit de matematicieni intră într-un bar. Primul spune: „Voi bea un pahar de bere!” Al doilea: „Voi bea o jumătate de pahar de bere!” Al treilea: „Voi bea un sfert de pahar de bere!” Al patrulea: „Voi bea un pahar de bere!” Barman: „Stai puțin... Îți cunosc trucurile - ai două pahare de bere pentru toată lumea!”

Probleme de examen de stat unificat pentru soluții independente

1. Omul de afaceri Korovin a primit un profit de 1.400.000 de ruble în 2000. În fiecare an următor, profiturile sale au crescut cu 20% față de anul precedent. Câte ruble a câștigat Korovin în 2004?

2. Compania Alpha a început să investească într-o industrie promițătoare în 2001, cu un capital de 4.000 USD. În fiecare an, din 2002, a realizat un profit care a reprezentat 100% din capitalul anului precedent. Și Beta Company a început să investească într-o altă industrie în 2004, cu un capital de 4.500 USD și, din 2005, a realizat un profit anual de 200% din capitalul anului precedent. Cu câți dolari era capitalul unei companii mai mare decât capitalul celeilalte la sfârșitul anului 2007, dacă profiturile nu erau retrase din circulație?

Raspuns: 2 903 040
Răspuns: 134500

Popular

Descrierea generală a zodiei Totul despre zodia Gemeni

« Trăsături Gemeni Versatil și adaptabil; Sociabil și spiritual; Inteligent și elocvent; Activ si muncitor.... »

Informații contabile Stergerea combustibilului în 1s 8

« Pasul 1. Emiterea de fonduri pentru raport În primul rând, să vedem cum să reflectăm achiziția de combustibil și lubrifianți de către un angajat pentru numerar în 1C 8.3. În primul rând... »

Folosind grupuri de numere și serii

« Pentru ce se folosesc seriale de articole. Cum se țin cont de ele în program? »